Den 3

Intuice - věřit jí či nevěřit

Než se pustím dál v objevování toho, jak vést spokojenější a šťastnější život, je třeba vypořádat se s intuicemi. Tedy s těmi tušeními, které mám, aniž bych je měl podložené zřetelnými důvody. Takový ten vnitřní hlas, nebo pocit jistoty či vhledu, který vede k rychlým rozhodnutím.

Někdy je intuice založena na empirické zkušenosti a v takovém případě má velkou šanci být ve svém předvídání úspěšná. Zkušení manažeři to tak někdy mají. Ale třeba i zkušení řemeslníci. Já třeba fotím tanec a často dopředu tuším, že teď přijde skok, i když jsem tu choreografii nikdy neviděl. Viděl jsem ale spousty jiných choreografií a zřejmě vnímám celou tu situaci na scéně, hudbu či poznám přípravné kroky a pohyby. Ale nepřemýšlím o tom tak. To vše se stane velmi rychle. Bezmyšlenkovitě. Řekl bych: "Nějak vím, že teď skočí." Ale nevím. Je to intuice. Která mi v tomhle případě často vyjde.

 

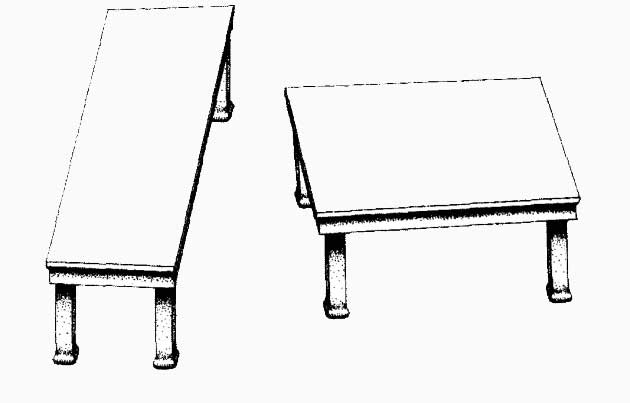
Koukni na obrázek s těmi stoly. Nepřemýšlej o nich jako o stolech v prostoru. Zaměř se jen na délky hran desek stolů (šířka a délka). Tak jak ty čáry na obrazovce vidíš. Jak moc se liší?

Roman, O. říká, že čára, která představuje šířku toho stolu vlevo je zhruba poloviční než u toho vpravo. Na druhou stranu délková hrana je prý tak o třetinu delší.

Lucie H. naopak říká, že má intuici, že to bude přesně naopak, než se zdá, protože se čtenáře snažím nachytat.

A to je ta zkušenost, o které jsem psal, a kterou máme všichni z podobných hádanek už od dětství. Vždy to u takových hádanek bylo jinak či opačně, než se zdálo na první pohled. Přesto v tom, že se někoho snažím nachytat, pravdu nemá. Chci jen ukázat, jak vnímání světa, které se zdá jasné a jisté, může být mylné.

Bez kontextu této kapitoly, pokud bychom se s takovou situací setkali sami, nepřemýšleli bychom o hádance a o tom, že nás chce někdo nachytat a odhadli to bez měření a přemýšlení. Intuitivně. S velkou pravděpodobnostní chybně.

  

Ale vraťme se k intuicím. Tedy k těm poznáním, chápáním či rozhodnutím, ve kterých jsme si poměrně jisti, přestože nejsou zprostředkovány vědomým uvažováním. Patří mezi ně i optické iluze. Ty také vyhodnocujeme bez přemýšlení či nějakého měření a zkoumání. Jejich celá řada. Jako třeba červené čáry na tom druhém obrázku. Zdají se různě dlouhé, přestože je jejich délka stejná.

Celá řada dalších optických iluzí je k vidění třeba zde: https://www.pcmag.com/news/21-optical-illusions-that-prove-your-brain-sucks

Jak možná tušíš, i ty stoly jsou optickou iluzí. Jde o jednu z těch nejsilnějších. Jsou to tzv. Shepard tables (v roce 1990 je publikoval Roger N. Shepard). Jaký poměr odhaduješ?

Přestože se délky hran desek stolů zdají radikálně rozdílné, jsou ve skutečnosti shodné. Můžu si je přeměřit. Nejen to. Sedí i úhly. Když obrázek vytisknu a desku jednoho stolu vystřihnu, lze ji otočit a bude přesně pasovat na ten druhý. Schválně, zkus to. Já to vyzkoušel. I když si vše ověřím a vím to, nezamezím tomu, že je vidím rozdílné. Wau! To je zásadní zjištění.

Foto: Oscar Keys

Ani znalost nezabrání tomu, abych svět vnímal jinak, než jaký ve skutečnosti je.

To jak může být naše mysl ošálena či přesvědčena o nesprávném se netýká jen optických iluzí.

Existuje něco, čemu se říká heuristika dostupnosti. To je druh zkreslení v myšlenkovém zpracování informací, které je charakteristické tím, že máme tendenci přemýšlet a rozhodovat na základě informací, které máme k dispozici, které si snadno vybavíme.

Amos Tversky a Daniel Kahneman (1974) mezi dalšími příklady uvádí, že když se ptali lidí, zda slova delších než 3 písmena začínají častěji na určité písmeno nebo toto písmeno obsahují na 3. pozici, volili lidé tu první variantu.
Tedy že je více slov, které tímto písmenem začínají. A to i pro písmena, kde tomu tak není. Připisují to tomu, že je mnohem snazší vybavit si slova začínající na určité písmeno, než slova obsahující toto písmeno na třetí pozici.

Pokud např. něco vidím v televizi, slyším o tom v rádiu, čtu o tom na internetu a bavím se o tom s přáteli, můžu mít dojem, že pravděpodobnost takové události je větší, než pravděpodobnost daleko častější události, která se takové pozornosti netěší. A to jen proto, že se s tím prvním jevem/informací setkávám často (i když jen zprostředkovaně) a snáze si jej tak vybavím.

Dalším typem je konfirmační zkreslení. To spočívá v tom, že mám tendenci upřednostňovat ty informace a výklady podporující můj vlastní názor a naopak podceňovat nebo i zcela pomíjet ty, které jsou s mým názorem v rozporu. Pokud se mi nějaký názor líbí, mám prostě tendenci mu věřit. Toto zkreslení má dokonce vliv i na paměť v tom smyslu, že si spíše zapamatuji ty informace a události, které můj již vytvořený názor podporují.

Na tato zkreslení se může nabalovat a souviset s nimi konzervativní zkreslení. Toto zkreslení se projevuje tak, že poté, co mám již vytvořený názor, který se mi zdá logický, obtížněji přijímám nové informace a obvykle je považuji za méně významné.

Pokud někdo na intuici hodně dá a věří jí, ať zde nebo v dalších kapitolách uvedu jekékoliv příklady a studie proti, bude jej to spíše dráždit, nebude se mu to zdát pravda, věřit tomu nejspíš nebude a brzy na to zapomene.

Existuje řada dalších zkreslení jako: Stádový efekt, informační zkreslení, zkreslení rámcováním atd. Nekladu si za cíl vyjmenovat zde všechna zkreslení, ale pouze ukázat, že je mnoho důvodů, proč mohou být naše přesvědčení a intuice mylné.

Foto: Lenora Cagle

Hele, co takhle ještě jednou otestovat sám sebe? Představ si, že jsi v obchodě. Baseballová pálka a míč se prodávají samostatně. Dohromady stojí 1100 Kč. Pálka je o 1000 Kč dražší než míč. Kolik stojí míč?

Hm? No tak, kolik? To přeci není tak těžké.

Ptal jsem se asi 10 běžných lidí se středním nebo vysokoškolským vzděláním. I když čekali chyták, všichni odpověděli, že míč stojí sto korun. "To je přece jasné." Ti, co odpovídali, to viděli jasně. Správná odpověď to ale není. Pokud si i teď myslíš, že to správná odpověď je, přestože píšu, že není, tak je to důkaz, jak velmi silná může špatná intuice být. Wow!

Lucka H. a teď už i Verča H. mě nabádají, abych zde prozradil, kolik tedy míč stojí a proč. A to hned. Ale já si to nechám na později. :)

Chceš ještě jeden příklad? Když bys z drátku udělal očko tak, aby ním těsně prošla kulečníková koule, bude mít nějakou délku. Když by měl projít o něco větší fotbalový míč, bude muset být drátek o kus delší. Představuješ si to?
Kdyby měla ta kulečníková koule velikost Země, měřil by takový drátek něco víc jak 40 074 kilometrů, tedy zhruba 40 074 156 metrů. Obrovská délka, co? A co kdybychom drátek nechtěli omotat těsně, ale tak, aby byl metr nad povrchem? O kolik metrů by musel být delší? Nepočítej to. Co Ti říká intuice? Zhruba.

Zjistil jsem právě, že moje intuice - jakkoliv silné - nemusí odpovídat realitě a nemůžu se jimi vždy spolehlivě řídit.

Znamená to, že musím vynaložit extra úsilí, abych svá rozhodnutí nezakládal na klamech a iluzích.